Nested call expressions

Anatomy of a call expression

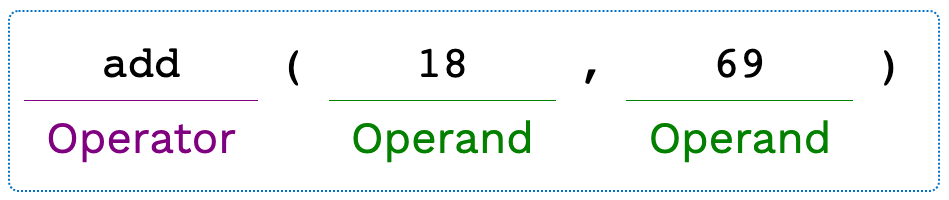
Before we dive into more complex call expressions, let's first understand a simple call expression more deeply. Remember, a call expression is any expression that calls a function, like pow(2, 100). The diagram below is for a call expression using the add function.

Here's how Python evaluates that call expression:

It first evaluates the operator. In this case, it sees that it's a function named add, checks to see if an add function is accessible in the current environment, and remembers whatever function definition it finds.
It then evaluates the operands, in order. Above, they are both simple numbers, so it first evaluates the number 18 and then the number 69. Since those are simple number values and not expressions themselves, it doesn't have to do much work here!
Finally, it applies the operator (a function) to the operands (values), according to the function definition. The above expression calls the add function on the values 18 and 69 and returns whatever is computed by that function.

🧠 Check Your Understanding

Is any additional code required for the above call expression to work?

No, add(18, 69) should work on its own.

This is incorrect. Since add comes from the operator module, it must be imported first. Otherwise Python does not know where to find the add function definition.

Yes, there needs to be an import statement below it.

Yes, there needs to be an import statement above it.

This answer is correct, there needs to be from operator import add before this line of code.

The add function is not actually one of the globally available built-in Python functions (like pow, max, min, and abs), so it must be imported from the operator module. There needs to be a line above the code, from operator import add.

Nested call expressions

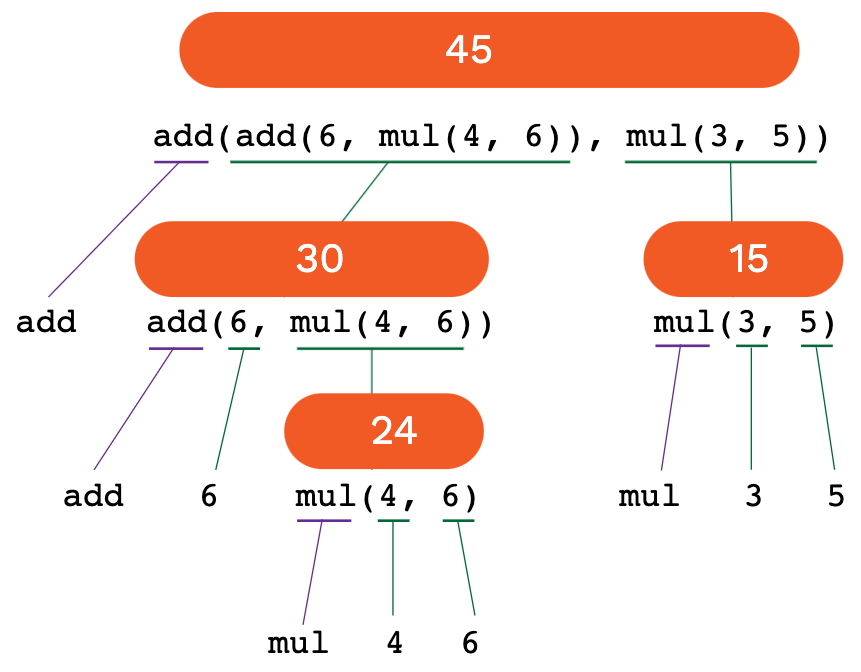
Now let's look at a nested call expression: a call expression where the expressions themselves are also call expressions.

If we were asked to evaluate that as a human, logically, we'd realize that we can't compute the outer add function until we know the operands, and we can't even compute that inner add function until we know the result of the first mul operation.

So we might start from the inside out, computing like this:

add(add(6, mul(4, 6)), mul(3, 5))
add(add(6,    24    ), mul(3, 5))
add(add(6,    24    ), mul(3, 5))
add(        30       , mul(3, 5))
add(        30       , mul(3, 5))
add(        30       ,    15    )
add(        30       ,    15    )
45

The computer takes a similar approach, creating an expression tree. It applies the same 3-step process from before to each call expression in the tree, starting with the bottom-most expressions, until it's able to finally do the final computation.

📺 Here's a video walkthrough of that call expression tree which shows the order of the calls and return values.

🧠 Check Your Understanding

What's the final step for that call expression?

Looking up the outer add function to make sure it's defined in the environment.

Calling the add function on the values 30 and 15

Calling the mul function on the values 4 and 6

Calling the add function on the values 6 and 24

Exercise: Operator expressions

The following expressions are written entirely with arithmetic operators. Rewrite them using the following functions from the operator module: add, sub, mul, truediv, floordiv, and mod. You may find this table that maps operators to functions particularly helpful.

30 + 2
30 - 2
30 * 2
30 / 2
30 // 2
30 % 2
30 + (2 * 4)
3 * (10 - 2)
(3 ** (365/52)) - 1
(25 // 4) - (25 / 4)

from operator import add, sub, mul, truediv, floordiv, mod # After adding a call expression, run code to see if its correct add(30, 2)

➡️ Next up: Names & Variables